I used to own a whole bunch of equipment – camera, lenses, lights – but for reasons I’ve detailed elsewhere I got rid of all that back in 2017. These days I travel pretty light (no pun intended) to set, but there are a few items I wouldn’t like to be without.
Here’s what’s in my set bag, roughly in descending order of importance.
1. Phone
Alright, this isn’t technically in my set bag, but it is the most used thing on a typical day on set. I use Chemical Wedding‘s Artemis Pro app all the time to find frames and select lenses, the same company’s Helios Pro to look at sun paths, and occasionally other specialist apps like Arri Photometrics (to work out if a particular light is powerful enough at a particular distance) and Flicker Finder (to check if a light will flicker on camera). I’ve also got Lux Calc installed but so far I’ve never used it.
Other common uses of my phone are looking at call sheets and other production documents if hardcopies aren’t supplied, checking my Google Sheets breakdown to remind myself of my creative intentions for the scene, and taking photos of lighting set-ups in case I need to recreate them for pick-ups.
To enable Artemis Pro to simulate wider lenses with my iPhone 7’s relatively tight built-in lens I also carry a clip-on 0.67x wide angle adaptor.
2. Light Meter
I’ve written before about why light meters are still important. My Sekonic L-758D gets heavy use on set, mostly in incident mode but sometimes the spot reflectance mode too; see my post on judging exposure to learn about what these modes do.
I make sure to carry spare batteries for it too.
3. Gaffer’s Glass
On The Little Mermaid the crew took pity on me using a broken ND filter wrapped in ND gel as a gaffer’s glass and bought me a proper one. This is like a monocle with an ND 3.6 filter in it for looking into fresnels and other directional fixtures to see if the spot of light is aimed exactly where it should be. I mostly use mine to look at the clouds and see when the sun is going to go in and come out, but you shouldn’t use one to look at the naked sun because even with all the ND it can still damage your eyes.
4. Power bank
With the heavy use my phone gets on set the charge doesn’t always last the whole day, so a power bank is essential to keep it running, as of course is the mains charger just in case.
5. Travel mug/flask
Most productions are environmentally conscious enough now to dissuade people from using disposable coffee cups and water bottes (though there are still a million half-finished water bottles on set at the end of the day). I always bring my own travel mug and metal water bottle. Keeping the mug clean(ish), especially when switching between tea and coffee consumption, is a daily struggle.
6. Croc clips
I always keep a couple of croc clips on my belt when shooting. Although I rarely gel lights myself on larger productions, I find them useful for adjusting curtains to admit just the right amount of daylight, or attaching a rain cover or light-blocking cloth to the camera, or clipping my jacket to something as a last-minute lighting flag.
7. Multi-tool
On some productions I’ve worn a multi-tool on my belt every day and only used it once or twice (usually to open wrap beers), so now it stays in my bag unless it’s specifically needed. As a head of department I theoretically shouldn’t be doing any tasks that would require a multi-tool, but it’s annoying to need one and not have one.
8. Tape Measure
I think my mum gave me this tiny tape measure which I keep in my set bag because it’s so small and light there’s no reason not to. I’ve used it exactly once so far: to work out if an Alexa Classic with a Cooke 10:1 zoom on would fit into certain tight locations on Hamlet.
9. Gel swatches
I picked up a set of Rosco filter swatches at either the BSC Expo or the Media Production Show. I don’t think I’ve ever used it.
10. Compass
Occasionally Helios Pro isn’t playing ball and I need to work out roughly where the sun is going to be, so out comes the traditional compass.
One final thing. Until very recently I carried a pair of gardening gloves for handling hot lights, but again I shouldn’t really be doing this myself and incandescent lamps aren’t too common on sets any more anyway, so when my gloves became worn out enough to need replacing I decided not to bother.






 To make the whole thing a little more fun and primitive, I decided to shoot using
To make the whole thing a little more fun and primitive, I decided to shoot using 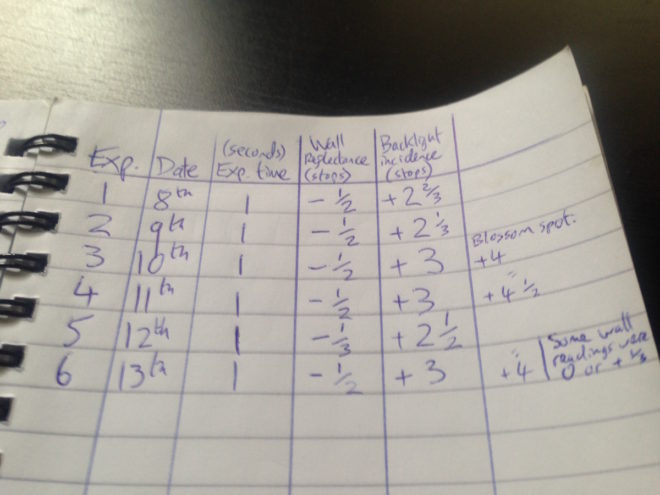

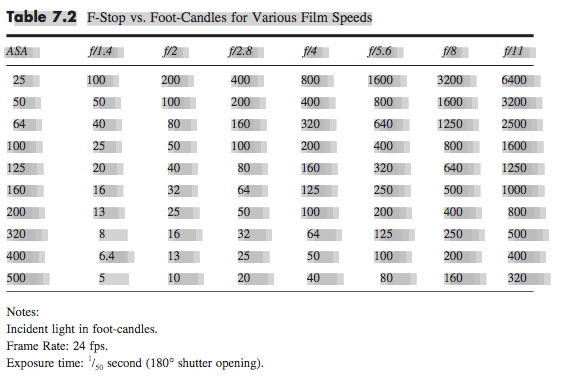

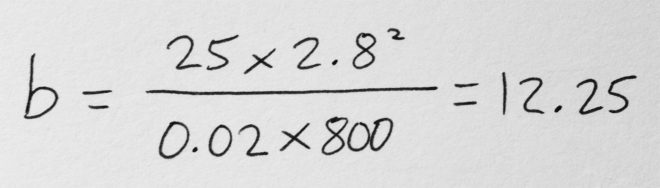




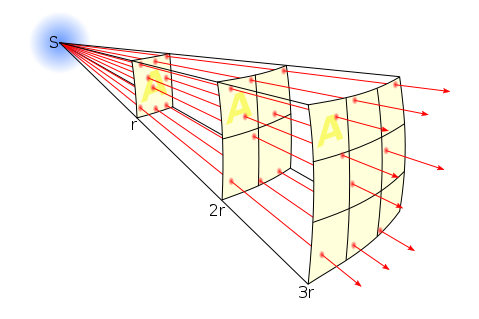
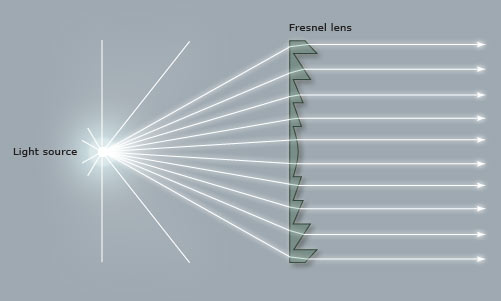
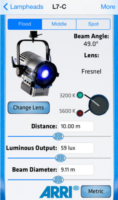 You can use data supplied by the lamp manufacturer to calculate the exposure it will provide, which is very useful in preproduction when deciding what size of lamps you need to hire. There are apps for this, such as the
You can use data supplied by the lamp manufacturer to calculate the exposure it will provide, which is very useful in preproduction when deciding what size of lamps you need to hire. There are apps for this, such as the  Some believe that light meters are unnecessary in today’s digital landscape, but I disagree. Most of the methods listed below require the camera, but the camera may not always be handy – on a location recce, for example. Or during production, it would be inconvenient to interrupt the ACs while they’re rigging the camera onto a crane or Steadicam. This is when having a light meter on your belt becomes very useful.
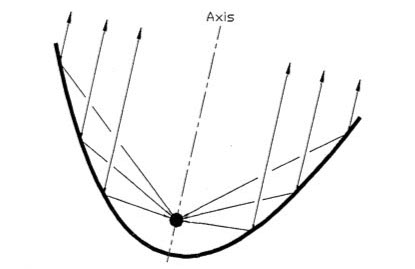
Some believe that light meters are unnecessary in today’s digital landscape, but I disagree. Most of the methods listed below require the camera, but the camera may not always be handy – on a location recce, for example. Or during production, it would be inconvenient to interrupt the ACs while they’re rigging the camera onto a crane or Steadicam. This is when having a light meter on your belt becomes very useful. Now we move along the light path and consider light after it has been reflected off the subject. This is what a spot meter measures. It has a viewfinder with which you target the area you want to read, and it is capable of metering things that would be impractical or impossible to measure with an incident meter. If you had a bright hillside in the background of your shot, you would need to drive over to that hill and climb it to measure the incident light; with a spot meter you would simply stand at the camera position and point it in the right direction. A spot meter can also be used to measure light sources themselves: the sky, a practical lamp, a flame and so on.
Now we move along the light path and consider light after it has been reflected off the subject. This is what a spot meter measures. It has a viewfinder with which you target the area you want to read, and it is capable of metering things that would be impractical or impossible to measure with an incident meter. If you had a bright hillside in the background of your shot, you would need to drive over to that hill and climb it to measure the incident light; with a spot meter you would simply stand at the camera position and point it in the right direction. A spot meter can also be used to measure light sources themselves: the sky, a practical lamp, a flame and so on. Your smartphone can be turned into a spot meter with a suitable app, such as
Your smartphone can be turned into a spot meter with a suitable app, such as 
 A waveform plots luminance on the vertical axis, with the horizontal axis matching the horizontal position of those luminance values within the frame. The density of the plotting reveals the prevalence of the values. A waveform that was dense in the bottom left, for example, would indicate a lot of dark tones on the lefthand side of frame. Since the vertical (luminance) axis represents IRE (Institute of Radio Engineers) values, waveforms are ideal when you need to expose to a given IRE, for example when calibrating a system by shooting a grey card. Another common example would be a visual effects supervisor requesting that a green screen be lit to 50 IRE.
A waveform plots luminance on the vertical axis, with the horizontal axis matching the horizontal position of those luminance values within the frame. The density of the plotting reveals the prevalence of the values. A waveform that was dense in the bottom left, for example, would indicate a lot of dark tones on the lefthand side of frame. Since the vertical (luminance) axis represents IRE (Institute of Radio Engineers) values, waveforms are ideal when you need to expose to a given IRE, for example when calibrating a system by shooting a grey card. Another common example would be a visual effects supervisor requesting that a green screen be lit to 50 IRE.